문제
명우는 홍준이와 함께 팰린드롬 놀이를 해보려고 한다.
먼저, 홍준이는 자연수 N개를 칠판에 적는다. 그 다음, 명우에게 질문을 총 M번 한다.
각 질문은 두 정수 S와 E(1 ≤ S ≤ E ≤ N)로 나타낼 수 있으며, S번째 수부터 E번째 까지 수가 팰린드롬을 이루는지를 물어보며, 명우는 각 질문에 대해 팰린드롬이다 또는 아니다를 말해야 한다.
예를 들어, 홍준이가 칠판에 적은 수가 1, 2, 1, 3, 1, 2, 1라고 하자.
- S = 1, E = 3인 경우 1, 2, 1은 팰린드롬이다.
- S = 2, E = 5인 경우 2, 1, 3, 1은 팰린드롬이 아니다.
- S = 3, E = 3인 경우 1은 팰린드롬이다.
- S = 5, E = 7인 경우 1, 2, 1은 팰린드롬이다.
자연수 N개와 질문 M개가 모두 주어졌을 때, 명우의 대답을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 수열의 크기 N (1 ≤ N ≤ 2,000)이 주어진다.
둘째 줄에는 홍준이가 칠판에 적은 수 N개가 순서대로 주어진다. 칠판에 적은 수는 100,000보다 작거나 같은 자연수이다.
셋째 줄에는 홍준이가 한 질문의 개수 M (1 ≤ M ≤ 1,000,000)이 주어진다.
넷째 줄부터 M개의 줄에는 홍준이가 명우에게 한 질문 S와 E가 한 줄에 하나씩 주어진다.
출력
총 M개의 줄에 걸쳐 홍준이의 질문에 대한 명우의 답을 입력으로 주어진 순서에 따라서 출력한다. 팰린드롬인 경우에는 1, 아닌 경우에는 0을 출력한다.
코딩 테스트 준비 - 연습
코딩 테스트 대비
code.plus
문제 이해
먼저 팰린드롬이라는 개념을 파악해야 문제에 접근할 수 있다.
숫자 혹은 문자로 이루어진 문자열에 대해 대칭일 때도 서로 같은 문자열을 띄우는 것이 팰린드롬이다.
예를 들어, a b b b a 를 대칭했을 때 마찬가지로 a b b b a 이므로 맞다!
반대로, a a b b a 는 대칭했을 때 a b b a a 이므로 서로 다르기 때문에 팰린드롬이 아니다.
팰린드롬을 구하기 위해 걸리는 시간 복잡도는 O(n)이다.
대칭구조를 이루면 되니
0번 째와 n-1번 째와 비교해서 같으면 true이고, 다르면 false이다.
다시 1번 째와 n-2번 째를 비교하는 로직을 구상한다면
총 n/2로 배열을 순환하므로 O(n/2) = O(n) 임을 알 수 있다.
이제 전체 시간복잡도를 잠시 살펴보자.

시간 제한이 0.5초이기 때문에, 1초당 1억이라면 5천만 정도를 만족하는 크기를 구해야 한다.
수열의 크기(N)는 최대 2,000
질문의 개수(M)는 최대 1,000,000
수열 전체에 대한 팰린드롬 (O(n)) 에 대해 질문의 개수마다 답을 출력 (O(m)) 해야 하므로
O(n) * O(m) = O(nm)
n * m = 2,000 * 1,000,000 = 2,000,000,000 (20억)
20억과 같은 크기로 0.5초 내에 구할 수 없음을 알게 된다.
그러면 어떻게 접근하면 좋을까?
Bottom Up 방식과 Top Down 방식으로 차근히 알아보겠다.
접근 방법
전체적인 구조는 다음의 형식을 따른다.
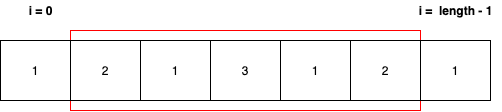
- 배열의 첫 번째 인자와 마지막 인자를 비교한다.
- 같다면 빨간 테두리 범위에 대해 1을 반복한다.
- 다르면 팰린드롬이 아니다.
변수 관련
dp = 다이나믹 프로그래밍을 이루기 위한 2차원 배열 (크기 : 2001 * 2001) (-1로 초기화)
a = 입력받은 수열
1. Bottom Up 방식
1. 부분 수열의 길이 = 1
이는 항상 팰린드롬을 만족하므로 dp에 1을 저장한다.
dp[i][i] = 1 (i = 0 until n)
2. 부분 수열의 길이 = 2
두 문자에 대해 같다면, 팰린드롬이므로 1을 저장
3. 그 이상 길이의 부분 수열일 경우
2부터 n까지의 길이(0번째부터이므로 2)를 순환해야 하는데 (k in 2 until n)
맨 처음과 끝의 원소에 대한 팰린드롬을 찾으려면
맨 처음 : i in 0 until n-k,
맨 끝 : j = i + k
예를 들어 1,2,3,2,1 의 수열에 대해 길이가 3인 경우를 찾는다고 해보자.
1, 2, 3 -> i = 0 , j = 2(0 + 2) 이므로 1,3 을 비교한다.
2, 3, 2 -> i = 1, j = 3(1 + 2) 이므로 2,2 를 비교한다.
그래서 i와 j에 대해, a[i] 와 a[j] 가 같고 dp[i+1][j-1]가 true였다면 dp[i][j] 역시 true가 된다.
Bottom Up을 이용한 코드
lateinit var a : IntArray
val dp = Array(2001) {IntArray(2001) {-1} }
fun main() = with(System.`in`.bufferedReader()) {
val n = readLine().toInt()
a = readLine().split(" ").map { it.toInt() }.toIntArray()
for(i in 0 until n) {
dp[i][i] = 1
}
for(i in 0 until n-1) {
if(a[i] == a[i+1])
dp[i][i+1] = 1
}
for(k in 2 until n) {
for(i in 0 until n - k) {
val j = i + k
if(a[i] == a[j] && dp[i+1][j-1] == 1)
dp[i][j] = 1
}
}
val bw = System.out.bufferedWriter()
val sb = StringBuilder()
repeat(readLine().toInt()) {
val (a,b) = readLine().split(" ").map { it.toInt() }
sb.appendLine(dp[a-1][b-1])
}
bw.write(sb.toString())
bw.flush()
bw.close()
}
2. Top Down 방식
질문에 따라 재귀함수를 호출하면 인자는 당연히 x, y (x부터 y까지) 로 받아야 한다.
단, 입력 조건에는 1부터 N까지 중의 숫자를 선택하므로 배열의 특성에 따라 x-1, y-1 로 받아야 한다.
재귀 호출의 종료 조건을 살펴보자.
1. x == y (부분 수열의 길이 : 1)
x와 y가 같은 경우는 똑같은 부분 수열의 위치를 가리킨다.
x = 1, y = 1 이라면 팰린드롬의 길이가 1이 되고, 이는 항상 팰린드롬을 만족한다.
그러므로 1을 반환한다.
2. x + 1 == y (부분 수열의 길이 : 2)
x + 1 과 y가 같다는 의미는 팰린드롬의 길이가 2를 가리킨다.
이는 특수한 경우를 의미하게 되는데, x != y 라고 해서 팰린드롬이 아니라고 false를 반환하게 되면
x = 2, y = 3 일 때 a[x] = 1, a[y] = 1 이면 true 인데 이를 false로 본다는 의미기 때문이다.
그렇기 때문에 해당 조건을 만족하면 a[x] == a[y] 가 같은지 확인한다.
맞으면 1, 틀리면 0을 반환한다.
3. dp[x][y] != -1
처음에 dp 배열을 -1로 초기화했을 때 재귀 조건에 따라 값이 채워질텐데,
만약 -1 이 아니라면 이미 index에 대한 최적의 값이 저장됐을 것이므로 memozation을 이용한다.
그러므로 dp[x][y]를 반환한다.
3. 부분 수열의 길이가 3 이상일 경우
a[x] 와 a[y] 가 같은 경우에는 팰린드롬을 충족하므로
dp[x][y] 에 재귀 함수 go(x+1, y-1) 로 다시 호출한다. 위에 작성한 전체적인 구조의 형식을 따른다.
a[x]와 a[y] 가 다른 경우에는 팰린드롬을 충족하지 않으므로
dp[x][y] = 0 을 넣어서 팰린드롬이 아님을 표시한다.
마지막으로 dp[x][y] 를 반환하면 올바른 재귀 호출을 이룰 수 있다.
Top Down을 이용한 코드
lateinit var a : IntArray
val dp = Array(2001) {IntArray(2001) {-1} }
fun main() = with(System.`in`.bufferedReader()) {
val n = readLine().toInt()
a = readLine().split(" ").map { it.toInt() }.toIntArray()
val bw = System.out.bufferedWriter()
val sb = StringBuilder()
repeat(readLine().toInt()) {
val (a,b) = readLine().split(" ").map { it.toInt() }
val ans = go(a-1, b-1)
sb.appendLine(ans)
}
bw.write(sb.toString())
bw.flush()
bw.close()
}
private fun go(x : Int, y : Int) : Int {
if(x==y) return 1
else if(x+1==y) {
return if(a[x] == a[y]) 1
else 0
}
if(dp[x][y] != -1)
return dp[x][y]
if(a[x] == a[y]) {
dp[x][y] = go(x+1, y-1)
} else {
dp[x][y] = 0
}
return dp[x][y]
}
시간 복잡도
위와 같은 방식으로 구현한다면
전체 N에 대해 N번째까지 구하므로 O(N^2) 이 되고,
M번의 질문에 따라 답을 출력해서 O(M)
그러므로 전체 시간 복잡도는 O(N^2 + M) 이 된다.
'algorithm > 다이나믹 프로그래밍' 카테고리의 다른 글
| 백준 9252) LCS 2 (0) | 2021.10.13 |
|---|---|
| 백준 2294) 동전 2 (0) | 2021.10.12 |
| 백준 9251) LCS (0) | 2021.05.06 |
| 백준 11053) 가장 긴 증가하는 부분 수열(LIS) (0) | 2021.05.01 |
| 백준 12865) 평범한 배낭 (0) | 2021.05.01 |
